Javascript required
Skip to content Skip to sidebar Skip to footer
Home / Draw a Box 72 by 46

Draw a Box 72 by 46

Descriptive Statistics

Box Plots

Box plots (also called box-and-whisker plots or box-whisker plots) requite a skilful graphical paradigm of the concentration of the data. They besides show how far the extreme values are from almost of the data. A box plot is synthetic from v values: the minimum value, the starting time quartile, the median, the third quartile, and the maximum value. Nosotros utilize these values to compare how close other information values are to them.

To construct a box plot, use a horizontal or vertical number line and a rectangular box. The smallest and largest information values label the endpoints of the axis. The first quartile marks one cease of the box and the tertiary quartile marks the other end of the box. Approximately the centre 50 percent of the data fall inside the box. The "whiskers" extend from the ends of the box to the smallest and largest data values. The median or 2d quartile tin can be betwixt the first and third quartiles, or information technology can be one, or the other, or both. The box plot gives a good, quick film of the data.

NOTE

You may encounter box-and-whisker plots that have dots marking outlier values. In those cases, the whiskers are not extending to the minimum and maximum values.

Consider, again, this dataset.

one i 2 2 four 6 6.8 vii.ii viii viii.3 9 10 10 11.five

The first quartile is two, the median is seven, and the 3rd quartile is nine. The smallest value is one, and the largest value is 11.v. The following image shows the synthetic box plot.

NOTE

See the figurer instructions on the TI spider web site or in the appendix.

Horizontal boxplot's first whisker extends from the smallest value, 1, to the first quartile, 2, the box begins at the first quartile and extends to the third quartile, 9, a vertical dashed line is drawn at the median, 7, and the second whisker extends from the third quartile to the largest value of 11.5.

The two whiskers extend from the beginning quartile to the smallest value and from the 3rd quartile to the largest value. The median is shown with a dashed line.

Annotation

Information technology is important to start a box plot with a scaled number line. Otherwise the box plot may not be useful.

The following data are the heights of 40 students in a statistics class.

59 threescore 61 62 62 63 63 64 64 64 65 65 65 65 65 65 65 65 65 66 66 67 67 68 68 69 70 70 70 70 70 71 71 72 72 73 74 74 75 77

Construct a box plot with the following properties; the figurer intructions for the minimum and maximum values likewise equally the quartiles follow the example.

  • Minimum value = 59
  • Maximum value = 77
  • Q1: First quartile = 64.5
  • Qtwo: Second quartile or median= 66
  • Qiii: 3rd quartile = 70

Horizontal boxplot with first whisker extending from smallest value, 59, to Q1, 64.5, box beginning from Q1 to Q3, 70, median dashed line at Q2, 66, and second whisker extending from Q3 to largest value, 77.

  1. Each quarter has approximately 25% of the information.
  2. The spreads of the four quarters are 64.5 – 59 = 5.5 (first quarter), 66 – 64.5 = i.5 (second quarter), 70 – 66 = four (third quarter), and 77 – lxx = 7 (fourth quarter). And then, the second quarter has the smallest spread and the fourth quarter has the largest spread.
  3. Range = maximum value – the minimum value = 77 – 59 = 18
  4. Interquartile Range: IQR = Q3 – Q1 = 70 – 64.v = 5.5.
  5. The interval 59–65 has more than than 25% of the data so it has more data in information technology than the interval 66 through 70 which has 25% of the data.
  6. The middle 50% (middle half) of the information has a range of 5.five inches.

To find the minimum, maximum, and quartiles:

Enter information into the list editor (Pres STAT one:EDIT). If you need to articulate the list, arrow upwards to the name L1, press Articulate, and then pointer down.

Put the information values into the list L1.

Press STAT and arrow to CALC. Press 1:1-VarStats. Enter L1.

Press ENTER.

Utilize the down and up pointer keys to scroll.

Smallest value = 59.

Largest value = 77.

Q i: First quartile = 64.5.

Q 2: Second quartile or median = 66.

Q 3: Third quartile = lxx.

To construct the box plot:

Printing 4:Plotsoff. Printing ENTER.

Pointer down and and so use the correct pointer fundamental to go to the fifth picture, which is the box plot. Press ENTER.

Arrow down to Xlist: Press 2nd 1 for L1

Arrow down to Freq: Press Alpha. Printing 1.

Press Zoom. Press 9: ZoomStat.

Printing TRACE, and use the arrow keys to examine the box plot.

Try It

The post-obit data are the number of pages in 40 books on a shelf. Construct a box plot using a graphing calculator, and state the interquartile range.

136 140 178 190 205 215 217 218 232 234 240 255 270 275 290 301 303 315 317 318 326 333 343 349 360 369 377 388 391 392 398 400 402 405 408 422 429 450 475 512

For some sets of data, some of the largest value, smallest value, beginning quartile, median, and third quartile may be the same. For instance, you might accept a data set in which the median and the 3rd quartile are the aforementioned. In this example, the diagram would not take a dotted line inside the box displaying the median. The correct side of the box would brandish both the 3rd quartile and the median. For instance, if the smallest value and the first quartile were both one, the median and the 3rd quartile were both five, and the largest value was 7, the box plot would wait like:

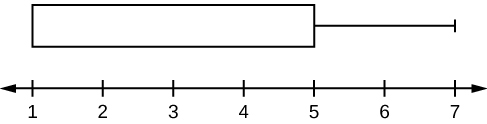
Horizontal boxplot box begins at the smallest value and Q1, 1, until the Q3 and median, 5, no median line is designated, and has its lone whisker extending from the Q3 to the largest value, 7.

In this case, at least 25% of the values are equal to one. Twenty-five pct of the values are between one and five, inclusive. At least 25% of the values are equal to five. The height 25% of the values autumn between v and seven, inclusive.

Test scores for a college statistics class held during the twenty-four hours are:

99 56 78 55.5 32 xc fourscore 81 56 59 45 77 84.5 84 70 72 68 32 79 ninety

Test scores for a college statistics class held during the evening are:

98 78 68 83 81 89 88 76 65 45 98 90 80 84.5 85 79 78 98 90 79 81 25.5

  1. Discover the smallest and largest values, the median, and the first and third quartile for the twenty-four hour period form.
  2. Observe the smallest and largest values, the median, and the commencement and third quartile for the nighttime class.
  3. For each information ready, what percentage of the data is betwixt the smallest value and the commencement quartile? the first quartile and the median? the median and the third quartile? the third quartile and the largest value? What percentage of the data is between the first quartile and the largest value?
  4. Create a box plot for each gear up of information. Use ane number line for both box plots.
  5. Which box plot has the widest spread for the middle 50% of the data (the data between the offset and third quartiles)? What does this mean for that set of data in comparison to the other set of information?
    • Min = 32
    • Q 1 = 56
    • Chiliad = 74.5
    • Q 3 = 82.5
    • Max = 99
    • Min = 25.5
    • Q i = 78
    • Thousand = 81
    • Q three = 89
    • Max = 98
  3. Day class: In that location are half-dozen data values ranging from 32 to 56: thirty%. There are six data values ranging from 56 to 74.5: 30%. There are five data values ranging from 74.5 to 82.5: 25%. There are five data values ranging from 82.five to 99: 25%. In that location are 16 data values betwixt the kickoff quartile, 56, and the largest value, 99: 75%. Dark form:

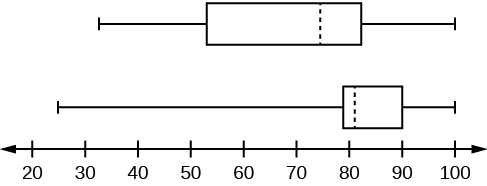
  4. Two box plots over a number line from 0 to 100. The top plot shows a whisker from 32 to 56, a solid line at 56, a dashed line at 74.5, a solid line at 82.5, and a whisker from 82.5 to 99. The lower plot shows a whisker from 25.5 to 78, solid line at 78, dashed line at 81, solid line at 89, and a whisker from 89 to 98.

  5. The kickoff data ready has the wider spread for the heart 50% of the data. The IQR for the beginning data prepare is greater than the IQR for the second set. This means that there is more variability in the middle 50% of the showtime information set.

Endeavour It

The post-obit data fix shows the heights in inches for the boys in a class of xl students.

66; 66; 67; 67; 68; 68; 68; 68; 68; 69; 69; 69; 70; 71; 72; 72; 72; 73; 73; 74
The following data set shows the heights in inches for the girls in a class of twoscore students.
61; 61; 62; 62; 63; 63; 63; 65; 65; 65; 66; 66; 66; 67; 68; 68; 68; 69; 69; 69
Construct a box plot using a graphing calculator for each information set, and country which box plot has the wider spread for the center 50% of the information.

Graph a box-and-whisker plot for the data values shown.

x 10 10 15 35 75 xc 95 100 175 420 490 515 515 790

The five numbers used to create a box-and-whisker plot are:

  • Min: x
  • Q ane: 15
  • Med: 95
  • Q 3: 490
  • Max: 790

The following graph shows the box-and-whisker plot.

Try Information technology

Follow the steps you used to graph a box-and-whisker plot for the data values shown.

0 5 5 15 30 30 45 50 fifty 60 75 110 140 240 330

Chapter Review

Box plots are a blazon of graph that can assistance visually organize data. To graph a box plot the following information points must be calculated: the minimum value, the commencement quartile, the median, the 3rd quartile, and the maximum value. One time the box plot is graphed, y'all tin can display and compare distributions of information.

Apply the following information to answer the adjacent two exercises. Threescore-five randomly selected car salespersons were asked the number of cars they mostly sell in 1 week. Fourteen people answered that they mostly sell three cars; nineteen generally sell four cars; twelve mostly sell v cars; nine generally sell half-dozen cars; eleven mostly sell seven cars.

Construct a box plot below. Employ a ruler to measure and scale accurately.

Looking at your box plot, does it announced that the data are full-bodied together, spread out evenly, or concentrated in some areas, merely not in others? How can y'all tell?

More than 25% of salespersons sell four cars in a typical week. Yous can see this concentration in the box plot because the first quartile is equal to the median. The peak 25% and the bottom 25% are spread out evenly; the whiskers have the same length.

Homework

In a survey of 20-twelvemonth-olds in China, Germany, and the United States, people were asked the number of strange countries they had visited in their lifetime. The following box plots display the results.

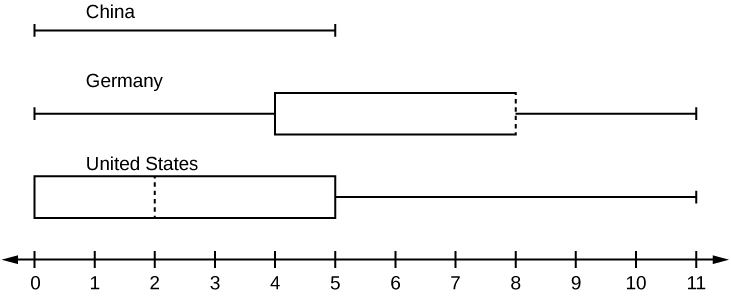
This shows three boxplots graphed over a number line from 0 to 11. The boxplots match the supplied data, and compare the countries' results. The China boxplot has a single whisker from 0 to 5. The Germany box plot's median is equal to the third quartile, so there is a dashed line at right edge of box. The America boxplot does not have a left whisker.

  1. In complete sentences, describe what the shape of each box plot implies almost the distribution of the data collected.
  2. Have more Americans or more than Germans surveyed been to over eight foreign countries?
  3. Compare the three box plots. What do they imply about the foreign travel of twenty-year-onetime residents of the 3 countries when compared to each other?

Given the post-obit box plot, answer the questions.

This is a boxplot graphed over a number line from 0 to 150. There is no first, or left, whisker. The box starts at the first quartile, 0, and ends at the third quartile, 80. A vertical, dashed line marks the median, 20. The second whisker extends the third quartile to the largest value, 150.

  1. Think of an example (in words) where the information might fit into the above box plot. In 2–5 sentences, write down the example.
  2. What does it hateful to take the starting time and second quartiles so shut together, while the second to third quartiles are far autonomously?
  1. Answers will vary. Possible answer: State University conducted a survey to see how involved its students are in community service. The box plot shows the number of community service hours logged by participants over the past yr.
  2. Because the commencement and second quartiles are close, the data in this quarter is very similar. At that place is not much variation in the values. The information in the third quarter is much more variable, or spread out. This is articulate because the second quartile is so far abroad from the third quartile.

Given the post-obit box plots, answer the questions.

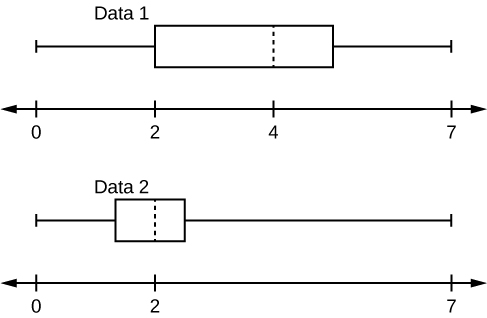
This shows two boxplots graphed over number lines from 0 to 7. The first whisker in the data 1 boxplot extends from 0 to 2. The box begins at the firs quartile, 2, and ends at the third quartile, 5. A vertical, dashed line marks the median at 4. The second whisker extends from the third quartile to the largest value, 7. The first whisker in the data 2 box plot extends from 0 to 1.3. The box begins at the first quartile, 1.3, and ends at the third quartile, 2.5. A vertical, dashed line marks the medial at 2. The second whisker extends from the third quartile to the largest value, 7.

  1. In consummate sentences, explicate why each statement is fake.
    1. Data 1 has more data values above two than Information 2 has above 2.
    2. The information sets cannot accept the same mode.
    3. For Data 1, there are more than data values below four than in that location are in a higher place 4.
  2. For which grouping, Data one or Data 2, is the value of "7" more probable to be an outlier? Explain why in consummate sentences.

A survey was conducted of 130 purchasers of new BMW 3 series cars, 130 purchasers of new BMW 5 series cars, and 130 purchasers of new BMW 7 series cars. In it, people were asked the age they were when they purchased their car. The following box plots display the results.

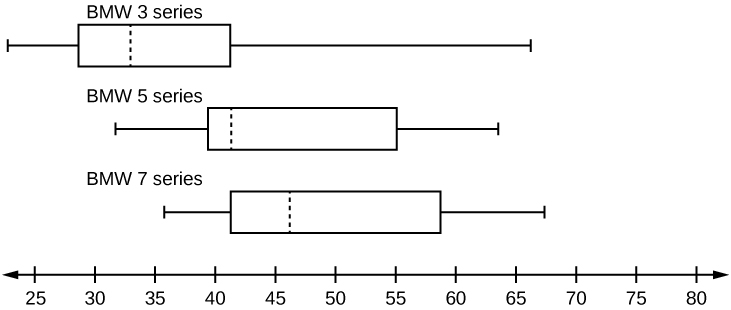
This shows three boxplots graphed over a number line from 25 to 80. The first whisker on the BMW 3 plot extends from 25 to 30. The box begins at the firs quartile, 30 and ends at the thir quartile, 41. A verical, dashed line marks the median at 34. The second whisker extends from the third quartile to 66. The first whisker on the BMW 5 plot extends from 31 to 40. The box begins at the firs quartile, 40, and ends at the third quartile, 55. A vertical, dashed line marks the median at 41. The second whisker extends from 55 to 64. The first whisker on the BMW 7 plot extends from 35 to 41. The box begins at the first quartile, 41, and ends at the third quartile, 59. A vertical, dashed line marks the median at 46. The second whisker extends from 59 to 68.

  1. In consummate sentences, depict what the shape of each box plot implies about the distribution of the data collected for that motorcar serial.
  2. Which group is almost probable to have an outlier? Explain how you determined that.
  3. Compare the 3 box plots. What do they imply about the age of purchasing a BMW from the series when compared to each other?
  4. Look at the BMW v series. Which quarter has the smallest spread of data? What is the spread?
  5. Wait at the BMW 5 series. Which quarter has the largest spread of information? What is the spread?
  6. Look at the BMW v series. Gauge the interquartile range (IQR).
  7. Await at the BMW five series. Are in that location more data in the interval 31 to 38 or in the interval 45 to 55? How do you know this?
  8. Look at the BMW five serial. Which interval has the fewest information in it? How do you lot know this?
    1. 31–35
    2. 38–41
    3. 41–64
  1. Each box plot is spread out more in the greater values. Each plot is skewed to the correct, so the ages of the top 50% of buyers are more than variable than the ages of the lower 50%.
  2. The BMW 3 serial is most likely to have an outlier. It has the longest whisker.
  3. Comparing the median ages, younger people tend to buy the BMW 3 series, while older people tend to buy the BMW 7 series. Yet, this is not a rule, considering there is and then much variability in each data set.
  4. The second quarter has the smallest spread. There seems to be only a iii-year difference between the first quartile and the median.
  5. The third quarter has the largest spread. At that place seems to be approximately a 14-twelvemonth difference between the median and the 3rd quartile.
  6. IQR ~ 17 years
  7. There is not enough information to tell. Each interval lies within a quarter, and so we cannot tell exactly where the information in that quarter is concentrated.
  8. The interval from 31 to 35 years has the fewest data values. 20-v pct of the values fall in the interval 38 to 41, and 25% fall between 41 and 64. Since 25% of values autumn between 31 and 38, we know that fewer than 25% fall between 31 and 35.

Twenty-five randomly selected students were asked the number of movies they watched the previous calendar week. The results are as follows:

# of movies Frequency
0 5
1 nine
2 6
three four
4 ane

Construct a box plot of the information.

Bringing Information technology Together

Santa Clara County, CA, has approximately 27,873 Japanese-Americans. Their ages are as follows:

Age Grouping Percent of Customs
0–17 eighteen.9
eighteen–24 8.0
25–34 22.8
35–44 15.0
45–54 xiii.i
55–64 11.9
65+ 10.three
  1. Construct a histogram of the Japanese-American community in Santa Clara County, CA. The confined volition not be the same width for this example. Why not? What impact does this take on the reliability of the graph?
  2. What percentage of the community is under age 35?
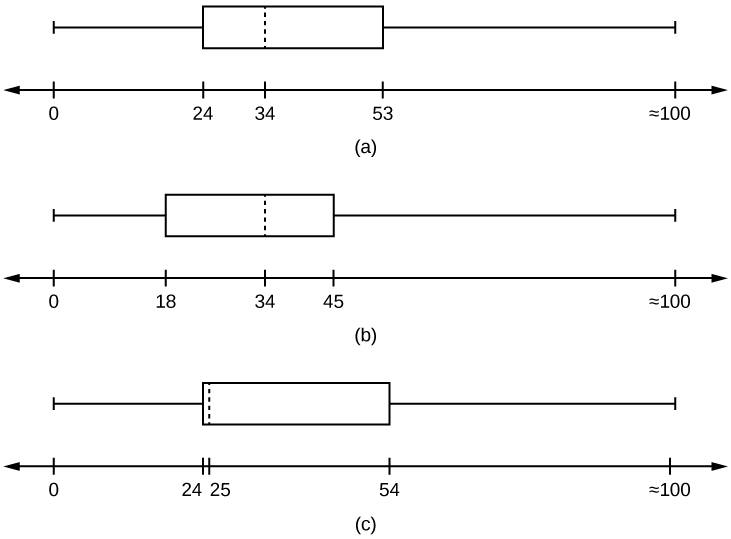
  3. Which box plot most resembles the information to a higher place?

Three box plots with values between 0 and 100. Plot i has Q1 at 24, M at 34, and Q3 at 53; Plot ii has Q1 at 18, M at 34, and Q3 at 45; Plot iii has Q1 at 24, M at 25, and Q3 at 54.

  1. For graph, bank check student's solution.
  2. 49.7% of the community is under the age of 35.
  3. Based on the information in the table, graph (a) near closely represents the data.

Glossary

Box plot
a graph that gives a quick picture of the middle 50% of the data
Offset Quartile
the value that is the median of the of the lower one-half of the ordered data gear up
Frequency Polygon
looks like a line graph but uses intervals to display ranges of large amounts of data
Interval
besides chosen a class interval; an interval represents a range of information and is used when displaying large information sets
Paired Data Set
ii data sets that have a i to ane human relationship so that:
  • both information sets are the aforementioned size, and
  • each data point in one information gear up is matched with exactly one point from the other set.
Skewed
used to describe data that is not symmetrical; when the right side of a graph looks "chopped off" compared the left side, nosotros say it is "skewed to the left." When the left side of the graph looks "chopped off" compared to the right side, we say the data is "skewed to the right." Alternatively: when the lower values of the information are more than spread out, we say the data are skewed to the left. When the greater values are more spread out, the data are skewed to the right.

ringrosewive1957.blogspot.com

Source: https://opentextbc.ca/introstatopenstax/chapter/box-plots/